21. Determinado terreno foi
dividido em dois lotes, A e B, conforme a figura a
seguir:
As medidas x, y e z são,
respectivamente,
a. x
= 4, y = 2 e z = 8.
b. x
= 8, y = 4 e z = 2.
c. x
= 8, y = 2 e z = 4.
d. x
= 10, y = 4 e z = 3.
e. x
= 12, y = 8 e z = 10.
22. Um
casal de namorados trabalha na mesma empresa, mas tem tido dificuldades de se
encontrar nos dias de folga: Maria Isabel tem uma folga a cada 5 dias, e
Filippe tem duas a cada 6 dias. Sabendo que a última Folga comum aos dois
foi no dia 28 de março, eles voltarão a tirar folga no mesmo dia em
a. 21 de
abril. b. 25 de abril. c. 27 de abril.
d. 07 de maio. e. 15 de maio.
23. O
hidrômetro é um aparelho com que se mede a quantidade de água consumida nas
residências. A leitura de um desses aparelhos, feita em determinado mês,
assinalou 956 m³. Um mês depois, a leitura do mesmo hidrômetro
indicou 1.021 m³ e, no mês seguinte, o aparelho indicou 1.050 m³.
Dado: 1 litro = 1 decímetro cúbico.
A média
do consumo de água nesse período é de
a. 1.009
litros. b. 10.009 litros. c. 100.090 litros. d. 100.900
litros. e. 1.009.000 litros.
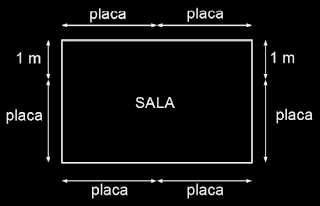
24. No
piso da sala retangular de um apartamento, cuja área é de 40 m², foi
comprado rodapé a partir de placas já pré-cortadas, de medida x,
além do que foi necessário para cobrir todo o perímetro. Observe o
desenho a seguir que representa a disposição do rodapé na sala:
A medida
de cada placa de rodapé é
a. 4
metros. b. 5 metros. c. 6 metros.
d. 7 metros. e. 8 metros.
25. Um
caminhão transporta uma mistura de álcool e água em quantidades proporcionais a
5 : 2. Sabendo que o caminhão está carregado e que a mistura possui 1.920
litros de água, a quantidade de álcool é de
a. 9.600
litros. b. 6.720 litros. c. 4.800 litros.
d. 3.840 litros. e. 1.920 litros.
26.
Dentre os 360 concorrentes às vagas de diplomata no Instituto Rio Branco,
exatamente 136 falam francês, 216 falam alemão, e outros 64 não falam
francês nem alemão. O número de concorrentes que falam as
duas línguas, francês e alemão, é
a. 224.
b. 144. c. 142.
d. 56. e. 52.
27.
Sabe-se que em certo polígono regular a medida de cada um de seus ângulos
externos é 72º. Assim, tal polígono possui
a. 8
lados. b. 7 lados. c. 6
lados. d. 5 lados. e. 4
lados.
28. As
TVs de LED são assim chamadas por possuírem uma iluminação traseira por LEDs –
diodos emissores de luz – considerada alta tecnologia e uma opção mais
sustentável entre as outras tecnologias de TVs, no que diz respeito
ao consumo de energia. Assim, como as demais TVs, mede-se o número de
polegadas da TV de LED a partir de um cálculo simples: é a medida da
diagonal da tela dividida por 2,54 cm (medida de
uma polegada).
Sabendo
que as dimensões da tela de uma TV de LED são 700 mm por 42 mm,
conclui-se que essa TV apresenta
a. 20
polegadas. b. 25 polegadas. c. 32 polegadas. d. 38
polegadas. e. 42 polegadas.
29. Para
uma festa de música eletrônica, foram reservadas três áreas distintas, de modo
que cada uma delas fosse ocupada por uma tenda, segundo as características
a seguir.
Área 1:
um quadrado de lado medindo 3x²;
Área 2:
um retângulo de dimensões x + 3 e x + 2;
Área 3:
um triângulo retângulo de catetos medindo x² e x + 3.
Se x
= 5 m, a área total ocupada por tais tendas será de
a. 5.625 m².
b. 5.725 m². c. 5.781 m².
d. 6.071 m². e. 6.081 m².
30. Um
fogão era vendido em 12 parcelas iguais de R$ 39,92 ou, mediante pagamento à
vista, com um desconto de R$ 30,54 que representa 6 % sobre o seu valor. O
preço do fogão para pagamento à vista é
a. R$
448,50. b. R$ 478,46. c. R$ 480,04.
d. R$ 509,00. e. R$ 590,00.
31. Duas
embarcações partem do mesmo ponto A, com intenção de chegarem a
destinos diferentes B e C, conforme
representação a seguir.
Partindo
do ponto A, a distância que a embarcação percorreu até o ponto C
foi de, aproximadamente,
a. 14,3 m.
b. 15,5 m. c. 16,9 m.
d. 18,3 m. e. 20,5 m.
32. A
quantidade de papel necessária para cobrir uma lata cilíndrica planificada de
dimensões conforme figura a seguir será de
a. 282,60
cm². b. 301,44 cm². c. 319,42 cm².
d. 339,12 cm². e. 340,50 cm².
33. Numa
tradicional prova do circuito de corridas de rua, os três primeiros colocados
recebem prêmios em dinheiro. Da quantia total a ser distribuída, metade
corresponde ao prêmio do 1º colocado, 35 % ao prêmio o 2º colocado e
R$ 6.000,00 ao do 3º colocado. Considerando que no câmbio atual um dólar
americano corresponda a aproximadamente R$ 2,00, o valor total da
premiação de tal prova é de
a. 20 mil
dólares.
b. 40 mil
dólares.
c. 60 mil
dólares.
d. 80 mil
dólares.
e. 100
mil dólares.
34.
Rubens, Carlos e Marcelo querem repartir entre eles 37 figurinhas, de modo que
Rubens receba 4 a mais que Carlos e este 3 a mais que Marcelo. Rubens,
Carlos e Marcelo receberão, respectivamente,
a. 9, 12
e 16 figurinhas.
b. 12, 9
e 16 figurinhas.
c. 12, 16
e 9 figurinhas.
d. 16, 9
e 12 figurinhas.
e. 16, 12
e 9 figurinhas.
35. Dados
os conjuntos
são, respectivamente,
36. Para
preparar fantasias, uma escola de samba contratou 3 grupos de profissionais.
Cada grupo estava incumbido de fazer determinada quantidade de fantasias
conforme tabela a seguir.
Sabendo
que a quantidade de profissionais é proporcional à quantidade de fantasias
preparadas, conclui-se
que o
grupo B tem
a. 30
profissionais.
b. 13
profissionais.
c. 7
profissionais.
d. 5
profissionais.
e. 4
profissionais.
37. A expressão (a + b + c)² é equivalente a
a. (abc)².
b. a²
+ b² + c².
c. a²
+ b² + c² + 2abc.
d. a²
+ b² + c² + 2a + 2b + 2c).
e. a²
+ b² + c² + 2(ab + bc + ca).
38. Sejam
a e b dois números naturais. Sabendo que o máximo
divisor comum entre os dois é 9 e que o produto dos números é 972, o valor
máximo de a é
a. 36.
b. 54. c. 81.
d. 108. e. 162.
39. Num trapézio a base menor, a base média e a base maior medem,
respectivamente, x + 4, 2x + 5 e 5x - 2.
O valor da incógnita x nesse caso é
a. 2.
b. 3. c. 4.
d. 5. e. 13.


















.jpg)




